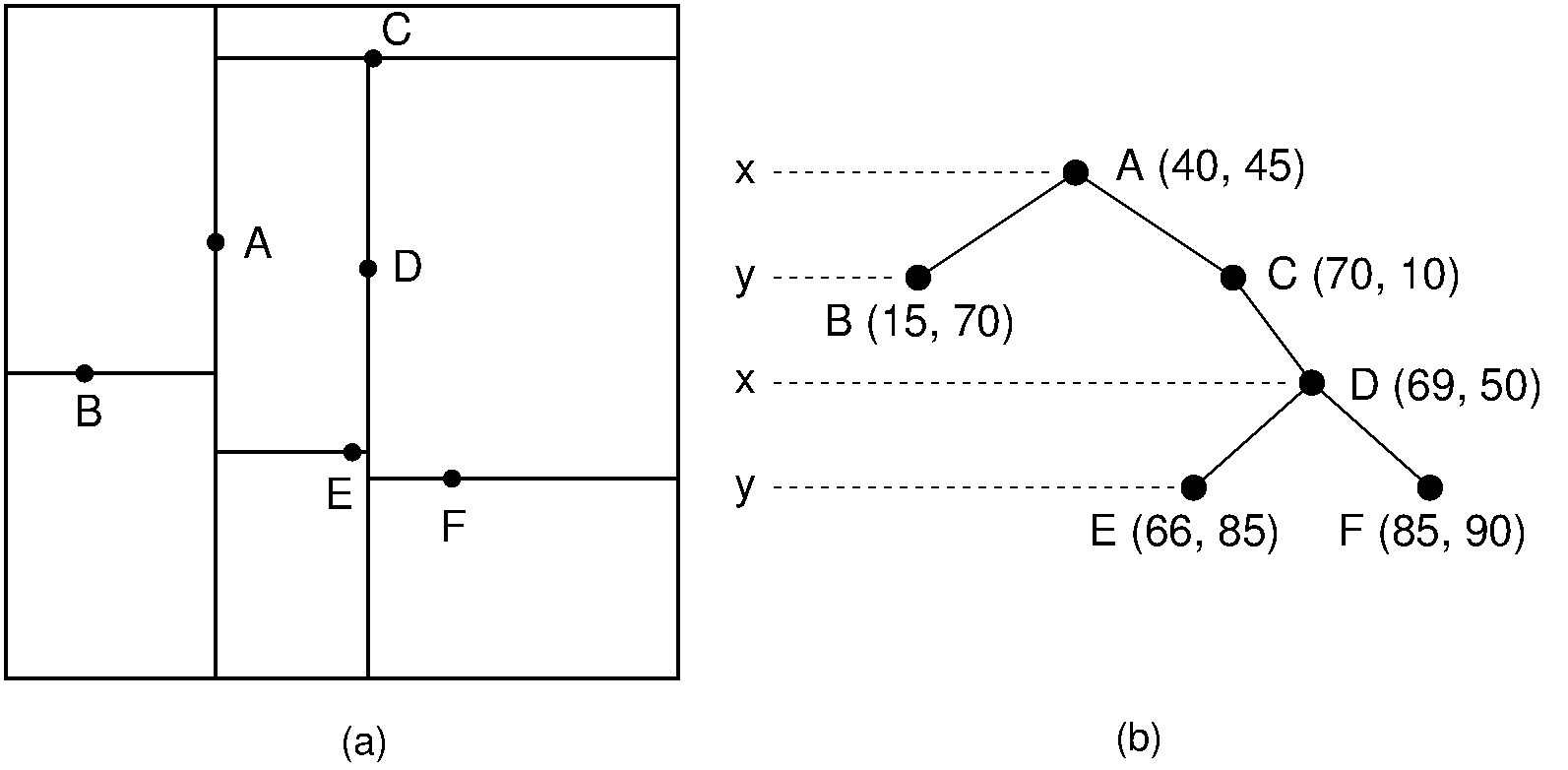
K Dimension Tree

In some cases we may be not interested in the question “is X in this container,” but rather “what value in the container is X most similar to?” At a high level, a kd-tree is a generalization of a binary search tree that stores points in k-dimensional space.

This is quoted from this nice introduction, and you can find more detailed interpretation in it. Here I just excerpt some contents from it.

When we just consider the balanced K-D tree, we always use median value to be split boundaries.

Nearest-Neighbor

• The first target should be in the smallest cell and we randomly choose one point in that cell, then we can construct a candidate hy- persphere centered at the test point and running through the guess point. The nearest neighbor to the test point must lie inside this hypersphere.
• If this hypersphere is fully to one side of a splitting hyperplane, then all points on the other side of the splitting hyperplane cannot be contained in the sphere and thus cannot be the nearest neighbor.
• To determine whether the candidate hypersphere crosses a splitting hyperplane that com- pares coordinate i, we check whether \(|b_i – a_i|<r\).
• If this hypersphere crosses some boundaries, we need to go back to the parent node (may go up to multiple upleavls). Then get a point to compute the distance and compare it with the previous distance.

This algorithm can be shown to run in O(log n) time on a balanced kd-tree with n data points provided that those points are randomly distributed. In the worst case, though, the entire tree might have to be searched. However, in low-dimensional spaces, such as the Cartesian plane or three-di- mensional space, this is rarely the case.

k-Nearest Neighbor Searches

We will apply K-D tree with a bounded priority queue (or BPQ for short) to tackle this problem. A bounded priority queue is similar to a regular priority queue, except that there is a fixed upper bound on the number of elements that can be stored in the BPQ. When- ever a new element is added to the queue, if the queue is at capacity, the element with the highest priority value is ejected from the queue.